martes, 3 de diciembre de 2013

Vista auxiliares

Vistas auxiliares

No siempre los planos que forman una pieza son paralelos a los planos de proyección. Cuando existen elementos oblicuos a los planos principales de proyección éstos se proyectan con deformación, no siendo sus proyecciones ortogonales aptas para las mediciones. Entonces se utilizan VISTAS AUXILIARES.Una vista auxiliar se emplea para mostrar la verdadera forma y magnitud de partes inclinadas de la pieza.
La vista auxiliar SIMPLE se obtiene cuando el plano de proyección auxiliar es perpendicular a uno de los principales.
La vista auxiliar simple equivale a un cambio de plano de proyección del sistema diédrico.

	La vista auxiliar simple se obtiene cuando el plano de proyección auxiliar V1, es perpendicular a uno de los principales, en este caso el horizontal H.
	La vista auxiliar simple equivale a un cambio de plano de proyección del sistema Diédrico.

Construcción de una vista auxiliar simple

	la vista auxiliar simple se coloca abatiendo el plano de la vista auxiliar V1 sobre el plano de la vista a la que es perpendicular el horizontal H.
	Esta abatimiento se realiza alrededor de la línea de intersección de los planos que es perpendicular a la flecha de la dirección de proyección.
	A la vista auxiliar ya abatida se le debe colocar una letra, la misma que a la flecha, para indicar como se ha obtenido
	Las vistas auxiliares se deben colocar siguiendo el orden del sistema empleado. En este caso es el europeo y la vista auxiliar se coloca al otro lado de la vista donde va la flecha, la planta.

	En la vista auxiliar la zona inclinada se ve en su verdadera forma, pero en las otras vistas, en esta caso el alzado, se ve deformada.
	Sin embargo la vista principal de la pieza se ve inclinada en la vista auxiliar y en verdadera forma en las otras vistas.
	En el proceso de construcción de la vista auxiliar se debe construir primero las zonas en verdadera forma y luego las formas deformadas a partir de las anteriores.
	La forma de construir una vista auxiliarse basa en el mantenimiento de las dimensiones entre las vistas. Así las alturas se ven en el alzado y en la vista auxiliar.

	la primera operación que hay que realizar es dibujar la base de la pieza en la planta y ene le alzado.
	Como se conoce el ángulo a, se puede dibujar la flecha A y orientar la vista auxiliar.
	Se pueden trazar las líneas entre las vistas y la bisectriz, si se emplea este método.
	Para situar el punto 1, se dibujan líneas desde las proyecciones del punto en la planta y alzado.
	Donde la línea del alzado cote a la bisectriz se traza la perpendicular a la flecha que se corta con la paralela a la flecha en el punto 1 de la vista auxiliar.

Llevando los puntos desde la planta y el alzado se construye la base de la pieza en la vista auxiliar.
	la zona inclinada se puede dibujar perfectamente en la vista auxiliar donde se ve en verdadera magnitud. En la planta se dibuja también la zona la zona.

	Con la vista auxiliar y la planta terminadas se puede construir la zona inclinada del alzado.
	Para ello se llevan puntos por ejemplo el punto 3, desde la vista auxiliar y la planta al alzado.
	los puntos se llevan usando líneas paralelas y perpendiculares a las direcciones de proyección y con la ayuda de la bisectriz.

figura Isometrico con todas sus vista y angulos

AXONOMETRÍA

La axonometría es uno de los tres Sistemas de representación del dibujo técnico o también denominado perspectivas paralelas es decir que se utiliza un solo observador ubicado en el infinito y cuyas visuales o proyectantes son todas paralelas entre sí, (conserva el paralelismo entre rectas).

Ofrece de inmediato la visión general de un objeto, tridimensional sobre el plano. El trazado de las perspectivas paralelas se realiza en su totalidad mediante un simple juego de escuadras y permiten mostrar plantas, alzados y secciones si fuera necesario en una misma imagen.
Es una de las herramientas fundamentales para la concreción de ideas permitiendo el rápido pasaje de la idea mental a la imagen gráfica.

Se pueden clasificar en ortogonales y clinogonales u oblicuas:
Dentro de las ortogonales tenemos la perspectiva Isométrica y la Isométrica en posición no isométrica.
Dentro de las clinogonales u oblicuas tenemos las perspectivas Cabinet y Cavallera.

Para que el dibujo se parezca más a la realidad, se aplica a veces un coeficiente de reducción en las medidas paralelas a los ejes de anchura y longitud (perspectiva cabinet)

Metodológicamente las más utilizadas en el que hacer diario de los contenidos curriculares son las perspectivas Isométricas, Cavalleras y Cabinet.

Perspectiva isométrica

La perspectiva isométrica es una técnica de representación gráfica de un objeto tridimensional en dos dimensiones, donde los tres ejes coordenados ortogonales al proyectarse forman ángulos iguales de 120º cada uno sobre el plano. Las dimensiones de los cuerpos paralelas a los ejes se representan a una misma escala.

lunes, 26 de julio de 2010

El nombre de la perspectiva, isométrica, deriva del griego y significa igual medida. Esto debido a que la escala de medición es la misma a lo largo de cada eje, cosa que no sucede con las otras perspectivas.
La perspectiva isométrica tiene la ventaja de permitir la representación a escala, pero sin reflejar la disminución aparente que produce la distancia entre el ojo humano y el objeto.
Los ejes de las X y de las Y se sitúan a 30º de la línea horizontal, pues son los que corresponden al plano horizontal. El eje Z se sitúa perpendicular la línea del horizonte, formando ángulos de 60º con los anteriores.

domingo, 25 de julio de 2010

Para comenzar, situamos los ejes coordenados:

• El eje OX, formando un ángulo de 30° con la horizontal, hacia la derecha.
• El eje OY, formando un ángulo de 30° con la horizontal, hacia la izquierda.
• El eje OZ, formando un ángulo de 90° con la horizontal, dirigido hacia arriba.

Para el trazado de los ejes se necesita un simple juego de escuadras.

La perspectiva isométrica no es un tipo de representación realista, ya que representa los objetos sin distorsionarlos, mientras que nosotros los percibimos distorsionados por la distancia; es decir, un mismo objeto lo percibimos pequeño si está lejos y grande si está cerca. Otra característica de este sistema es que siempre vamos a representar los objetos como vistos desde arriba.

sábado, 24 de julio de 2010

viernes, 23 de julio de 2010

EJERCICIO: Dadas las bases de 4 prismas determinar las alturas de cada uno de ellos, construyendo el agrupamiento en perspectiva isométrica.

trazado de curvas tecnicas

CURVAS TÉCNICAS

En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de

forma curva geométrica.

Si prestamos atención a nuestro entorno, nos damos cuenta de que en muchos de los objetos que nos

rodean están presentes las curvas técnicas y las curvas cónicas. Por ejemplo, desde la forma de parábola

que algunos ojos de puente tienen, hasta la forma de ovalo u ovoide con que se han diseñado ciertas

cucharas.

La naturaleza también contribuye a crear este tipo de formas; los meandros de algunos ríos, o el viento

al modelar las arenas de los desiertos dan testimonio de este tipo de figuras geométricas.

22.1 Curvas geométricas

Se define a una línea como curva geométrica cuando se aparta constantemente de la dirección recta sin

formar ángulos, y la trayectoria de los puntos que la forman es continua y, además, cumple una

determinada norma.

Existen dos grupos de curvas geométricas: las denominadas planas y las alabeadas.

Una curva recibe el nombre de plana cuando todos sus puntos están situados en un mismo plano; y

curva alabeada cuando cuatro de sus puntos no se encuentran en el mismo plano.

Dependiendo de la forma que tengan de generarse, las curvas planas se dividen en curvas técnicas y

curvas cónicas, que poseen propiedades específicas y distintas entre sí.

22.2 Curvas técnicas

Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean

éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.

Las curvas de este tipo se configuran mediante la unión de arcos de circunferencia que son tangentes

entre sí, dando lugar a la formación de figuras planas que pueden ser cerradas: óvalo, ovoide; o abiertas:

espirales, evolvente del círculo, etcétera.

22.2.1 Óvalo

22.2.1.1 Definición

Es una curva plana y cerrada, simétrica respecto a sus dos ejes perpendiculares y formada por cuatro

arcos de circunferencia iguales dos a dos.

Tiene dos ejes de simetría perpendiculares entre si

22.2.1.2 Construcción de óvalos

A continuación se desarrollan algunos de los trazados de óvalos más utilizados en dibujo técnico.

continuo, dete

Homotecia

Homotecia con centro O y λ>1.

Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro de la transformación.

Definición

Esquema de operación de una homotecia, en el plano euclídeo.

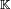Sea E un espacio vectorial sobre un cuerpo $\scriptstyle \mathbb{K}$ . Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada 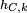$\scriptstyle h_{C, k}$ envía un punto M del espacio vectorial sobre el punto M' tal que:

(1a)

$M'- C = k(M-C)\,$

La ecuación anterior puede escribirse también como una transformación afín de la forma:

(1b)

$M' = kM + (1-k)C \,$

La anterior relación puede escribirse vectorialmente en el plano como:

$\begin{bmatrix} m'_x \\ m'_y\\ 1 \end{bmatrix} = \begin{bmatrix} k & 0 & (1-k)c_x \\ 0 & k & (1-k)c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} m_x \\ m_y\\ 1 \end{bmatrix}$

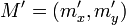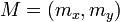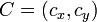Donde: $M' = (m'_x, m'_y)\,$ , $M = (m_x, m_y)\,$ y $C = (c_x, c_y)\,$ .
En tres o más dimensiones la fórmula anterior se generaliza trivialmente.

Cuando el cuerpo de escalares son los Reales, una homotecia de centro el punto C y razón el número real k ≠ 0, es una transformación geométrica que hace corresponder a cada punto P otro punto P′ tal que (el vector es igual al resultado de multiplicar el vector por el número k). Si k es positivo, P′ está en la semirrecta de origen C que pasa por P.

Propiedades

La homotecia es una transformación afín, composición de una transformación lineal y una traslación, y por consiguiente conserva:

el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura
el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C']
La imagen de una línea es otra línea paralela a la original.
el paralelismo: dos líneas paralelas tienen imágenes paralelas. En la figura (B'E') // (C'D') porque (BE) //(CD).
Si k ≠ 1, el centro de la homotecia es el único punto fijo (k = 1 corresponde a la identidad de E: todos los puntos son fijos).
k = - 1 corresponde a una simetría de centro C.
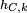Si k ≠ 0, $\scriptstyle h_{C, k}$ admite como trasformación recíproca $\scriptstyle h_{C, 1/k}$ (cuando k = 0, no es biyectiva).
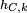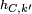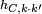Al componer dos homotecias del mismo centro se obtiene otra homotecia con este centro, cuya razón es el producto de las razones de las homotecias iniciales: $\scriptstyle h_{C, k}$ o $\scriptstyle h_{C, k'}$ = $\scriptstyle h_{C, k\cdot k'}$ .
Al componer homotecias de centros distintos, de razones k y k', se obtiene una homotecia de razón k·k' cuando k·k'≠1, y una traslación si k·k'=1. El conjunto de las homotecias (con k≠0) y las translaciones forman un grupo.

Cuando el cuerpo de escalares son los Reales, se cumple que:

todas las longitudes son multiplicadas por |k|, el valor absoluto de la razón.
el cociente de longitudes es conservado: A'C'/B'E' = AC/BE en la figura
los ángulos orientados son conservados, en particular los ángulos rectos. Es obvio en la figura.

Más aún:

k = - 1 corresponde a la simetría de centro C que es la rotación alrededor de C de ángulo π radianes (180º).
|k| > 1 implica una ampliación de la figura.
|k| < 1 implica una reducción.
k < 0, la homotecia se puede expresar como la composición de una simetría con una homotecia de razón |k|, ambas de igual centro. Que la homotecia original.

Homotecias en el plano real

En esta sección, los escalares serán números reales.

Una homotecia generalizada en el plano es una transformación del plano en sí mismo en donde una recta y su homóloga son paralelas. De esta definición, se sigue fácilmente que las homotecias conservan ángulos, es decir son transformaciones conformes del plano, que el conjunto de homotecias forman un 'grupo' y que las traslaciones son casos particulares de las homotecias.

Consideremos la homotecia en la cual la recta OA se transforma en la recta O'B, siendo O' el homólogo de O y B el homólogo de A. Necesariamente, las rectas OO' y AB son invariantes en esta homotecia y el punto H1, centro de la homotecia, es invariante. En esta homotecia la circunferencia de centro O y radio OA se transforma en la circunferencia de centro O' y de radio O'B y la razón de la homotecia es la razón (positiva) de los segmentos O'B y OA.

Si por el contrario, el punto A se transforma en B' entonces la recta AB' es invariante y es el punto H2 el centro de homotecia. En este caso, la razón de la homotecia es negativa.

Ejes de homotecia

Dadas dos circunferencias, éstas siempre se pueden considerar como homotéticas una de la otra.

En la figura, la circunferencia S2 puede considerarse homotética de s1 bien es en la homotecia de razón positiva, con centro en P1, o de razón negativa, con centro de homotecia en N1.

Consideremos las homotecias, una con centro en P1 en la cual la circunferencia S2 es homotética de la circunferencia s1, y la homotecia de centro P3 en la que la circunferencia s3 es homotética a la circunferencia s2. La composición de estas dos homotecias es la homotecia de centro en P2 que transforma la circunferencia s1 en la circunferencia s3. Es por esta razón que los centros de homotecia positivos, P1, P2 y P3 están alineados. En general, dadas tres circunferencias existen seis centros de homotecia, alineados tres a tres sobre cuatro rectas.